ten duotrigintillion . . .

[NoHall]

Is this gonna be on our end-of-the-year test?

 

[LightWorker]

Saying google makes me laugh....​

 

[greenroomsurfer]

Kurt ya have way to much time on your hands!!!!! Go put up some more stickers.:funn::rofl:

 

[rdelong43065]

Does this come before or after a gazillion?

 

[Kurt]

Does this come before or after a gazillion?

It's "gozillion" according to F Gump.

 

[Beach Runner]

Kurt is talking about finite numbers, even though they are large. You all need to know that there are much larger numbers.

Aleph-null (

) is by definition the cardinality ("size") of the set of all natural numbers, and (assuming, as usual, the axiom of choice) is the smallest of all infinite cardinalities. A set has cardinality

if and only if it is countably infinite, which is the case if and only if it can be put into a direct bijection, or "one-to-one correspondence", with the natural numbers. Such sets include the set of all integers. There are an infinite number of integers, but between any two successive integers there is no other integer.

The cardinality of the set of reals numbers is

. Between any two real numbers are an infinite number of real numbers. It follows from Zermelo-Fraenkel, ZFC, set theory that the celebrated continuim hypothesis, CH, is equivalent to the identity

CH is independent of ZFC: it can be neither proven nor disproven within the context of that axiom system. That it is consistent with ZFC was demonstrated by Kurt G?del in 1940; that it is independent of ZFC was demonstrated by Paul Cohen in 1963.

There are bigger numbers than aleph aero and aleph one -- there's aleph two, etc., etc.

I taught a course on this earlier this year.

 

[Miss Kitty]

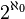
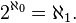
Oh my goodness....I would so flunk your course, BR!!! Those are some fancy symbol thingies you got there!

 

[SHELLY]

And now a word from the "Real World" of Finance:

Global nominal GDP is $48 Trillion.....

---------------------------------------------
Derivative Trades Jump 27% to Record $681 Trillion

Dec. 10 (Bloomberg) -- Derivatives traded on exchanges surged 27 percent to a record $681 trillion in the third quarter, the biggest increase in three years, the Bank for International Settlements said.

Interest-rate futures, contracts designed to speculate on or hedge against moves in borrowing rates, led the increase with a 31 percent increase to $594 trillion during the three months ended Sept. 30, the Basel, Switzerland-based BIS said today in its quarterly review. The amounts are based on the notional amount underlying the contracts.

Trading surged as investors bet on losses linked to record U.S. mortgage foreclosures and policy changes by the Federal Reserve and the European Central Bank to offset the credit slump. The Fed cut its benchmark interest rate by half a point to 4.75 percent in September, the central bank's first reduction in four years.

``The turbulence in financial markets led to the busiest trading on record,'' BIS analysts Ryan Stever, Christian Upper and Goetz von Peter wrote in the report.

Trading in stock index futures and options rose 19 percent to a record $81 trillion in the third quarter, as investors speculated on whether the credit-market losses would spread to the equity markets.

--------------------------------
Will we make it to a Quadrillion soon?

.

 

[DD]

is all I have to say about that.

 

[Kurt]

You all need to know that there are much larger numbers.